Light-industry-up.ru
Экосистема промышленности
Публикации
Национальный проект «Цифровая экономика»
Глобальный стандарт классификации отраслей
Росэлектроника
Электронная промышленность России
Категория:Предприятия лёгкой промышленности
Система маркировки и прослеживаемости товаров (Россия)
Электронные офисные системы
Категория:Предприятия лёгкой промышленности России
Экосистема цифровой экономики
Сколково (инновационный центр)
Векторный оператор лапласа физический смысл, векторный оператор лапласа в цилиндрических координатах, векторный оператор лапласа в криволинейной системе координат
27-04-2024
Ве́кторный опера́тор Лапла́са (или ве́кторный лапласиа́н) — это векторный дифференциальный оператор второго порядка, определённый над векторным полем и обозначаемый символом [1][2], аналогичный скалярному оператору Лапласа. Векторный оператор Лапласа действует на векторное поле и имеет векторное значение, тогда как скалярный лапласиан действует на скалярное поле и имеет скалярное значение. При вычислении в декартовых координатах, получаемое векторное поле эквивалентно векторному полю скалярного Лапласиана, действующего на отдельные компоненты исходного вектора.
- Поскольку векторный и скалярный лапласианы обозначаются одним и тем же символом, большой греческой буквой дельта, но являются разными математическими объектами, в рамках данной статьи векторный лапласиан обозначается черным цветом, а скалярный лапласиан — синим.
Определение
Векторный оператор Лапласа векторного поля определяется следующим образом:
- Через оператор набла:
- [3].
- Через градиент, дивергенцию и ротор:
- .
В декартовых координатах векторный лапласиан векторного поля можно представить в виде вектора, компонентами которого являются скалярные лапласианы компонент векторного поля :
- [1],
где , , — компоненты векторного поля .
Выражения для векторного оператора Лапласа в других системах координат можно найти в статье «Оператор набла в различных системах координат».
Обобщение
Лапласиан любого тензорного поля (скаляры и векторы являются частными случаями тензоров) определяется как дивергенция градиента тензора:
- .
В случае если — это скаляр (тензор нулевого порядка), оператор Лапласа принимает привычную форму.
Если — это вектор (тензор первого порядка), то его градиент это ковариантная производная, которая является тензором второго порядка, а его дивергенция — это снова вектор. Формула для векторного лапласиана может быть представлена как дивергенция выражения для градиента вектора:
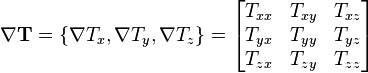 ,
,
где (общий вид компоненты тензора), и могут принимать значения из множества .
Аналогично, скалярное произведение вектора на градиент другого вектора (тензор второго порядка), значением которого является вектор, может быть рассмотрено как произведение матриц:
- .
Данное выражение зависит от системы координат.
Использование в физике
Примером использования векторного оператора Лапласа являются уравнения Навье — Стокса для идеальной несжимаемой жидкости[4]:
- ,
где слагаемое с векторными оператором Лапласа от поля скоростей представляет собой вязкость жидкости.
Литература
- Хмельник С.И. Уравнения Навье-Стокса существование и метод поиска глобального решения. — Израиль: MiC, 2010. — 106 с. — ISBN 978-0-557-48083-8.
Примечания
- ↑ 1 2 Хмельник, 2010, Приложение 1
- ↑ В отличии от скалярного оператора Лапласа, векторный оператор Лапласа не может обозначаться как квадрат оператора набла, поскольку он не является ни векторным, ни скалярным произведением оператора набла самого на себя:
- ,
- .
- Vector Laplacian (англ.) на сайте Wolfram MathWorld.
- ↑ Хмельник, 2010, Глава 2
| Дифференциальное исчисление | |||||||
|---|---|---|---|---|---|---|---|
| Основное | Производная • Дифференциал • Производная по направлению • Частная производная • Полная производная функции • Логарифмическая производная • Матрица Якоби • Матрица Гессе • Дифференциальная форма • Дифференциальное уравнение | ||||||
| Частные виды | Производная Ли • Производная Дини • Производная Пинкерля • Производная Римана • Ковариантная производная • Производная Пеано • Производная Радона — Никодима | ||||||
| Дифференциальные операторы (в различных координатах) |
|
||||||
| Связанные темы | Численное дифференцирование • Вариационное исчисление • Интеграл • Ряд Тейлора | ||||||
Векторный оператор лапласа физический смысл, векторный оператор лапласа в цилиндрических координатах, векторный оператор лапласа в криволинейной системе координат.
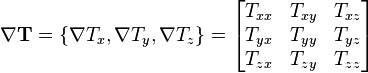 ,
,