Light-industry-up.ru
Экосистема промышленности
Публикации
Национальный проект «Цифровая экономика»
Глобальный стандарт классификации отраслей
Росэлектроника
Электронная промышленность России
Категория:Предприятия лёгкой промышленности
Система маркировки и прослеживаемости товаров (Россия)
Электронные офисные системы
Категория:Предприятия лёгкой промышленности России
Экосистема цифровой экономики
Сколково (инновационный центр)
Теорема Банаха о неподвижной точке
07-08-2023
Теорема Банаха о неподвижной точке — утверждение в метрической геометрии, гарантирующее наличие и единственность неподвижной точки у определённого класса отображений метрических пространств, также содержит конструктивный метод нахождения этой точки. Теорема названа в честь Стефана Банаха, польского математика, установившего это утверждение в 1922 году.
Теорема
Пусть — непустое полное метрическое пространство. Пусть — сжимающее отображение на , то есть существует число такое, что
для всех из . Тогда у отображения существует, и притом ровно одна неподвижная точка из (неподвижная означает ).
Число часто называют коэффициентом сжатия.
Если число равно 1, то есть отображение не сжимающее, теорема может не выполняться.
Доказательство
Возьмём произвольный и рассмотрим последовательность . Получим . Покажем, что эта последовательность фундаментальная. В самом деле:
- .
Таким образом, по неравенству треугольника для

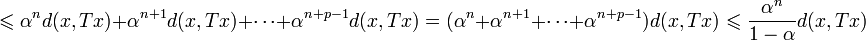 .
.
Но при , значит для .
Таким образом, для  .
.
Значит фундаментальна. Но так как полно, то . Тогда берём и переходим к пределу, так как сжимающий оператор — непрерывная функция. Существование доказано.
Докажем единственность. Предположим обратное, то есть пусть (так как и — неподвижные точки)  . Таким образом, доказана и единственность
. Таким образом, доказана и единственность
Применение
Теорема Банаха используется в теории дифференциальных уравнений для доказательства существования и единственности решения некоторых классов уравнений. Широкое применение теорема находит в численных методах, таких как метод Якоби, метод Гаусса — Зейделя, метод Ньютона также можно рассматривать с позиции теоремы Банаха. Также теорема нашла применение в теории фракталов.
Теорема Банаха о неподвижной точке.

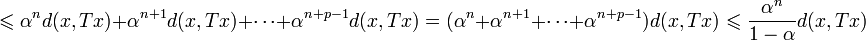 .
.