Light-industry-up.ru
Экосистема промышленности
Публикации
Национальный проект «Цифровая экономика»
Глобальный стандарт классификации отраслей
Росэлектроника
Электронная промышленность России
Категория:Предприятия лёгкой промышленности
Система маркировки и прослеживаемости товаров (Россия)
Электронные офисные системы
Категория:Предприятия лёгкой промышленности России
Экосистема цифровой экономики
Сколково (инновационный центр)
Кватернион
15-06-2023
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, образующее векторное пространство размерностью четыре над полем вещественных чисел. Кватернионы — минимальное расширение комплексных чисел, образующее тело, но их умножение некоммутативно. Предложена Гамильтоном в 1843 году, обычно обозначается .
Кватернионы удобны для описания изометрий трёх- и четырёхмерного Евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например при создании трёхмерной графики.[1]
Содержание |
Определения
Стандартное
Кватернионы можно определить как формальную сумму где — вещественные числа, а — мнимые единицы со следующим свойством: . Таким образом, таблица умножения базисных кватернионов — — выглядит так:
| · | ||||
например, , a .
Как Вектор&скаляр
Кватернион представляет собой пару где — вектор трёхмерного пространства, а — скаляр, то есть вещественное число. Операции сложения определены следующим образом:
Произведение определяется следующим образом:
где обозначает скалярное произведение, а — векторное произведение.
В частности,
Заметим, что
- Алгебраические операции в кватернионах обладают свойством дистрибутивности.
- Антикоммутативность векторного произведения влечёт некоммутативность произведения кватернионов.
Через комплексные числа
Кватернион можно представить как пару комплексных чисел. Пусть  и
и  . Тогда кватернион можно записать в виде
. Тогда кватернион можно записать в виде  .
.
Через матричные представления
Вещественными матрицами
Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:
При такой записи:
- сопряжённому кватерниону соответствует транспонированная матрица:
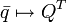 ;
;
- четвёртая степень модуля кватерниона равна определителю соответствующей матрицы:
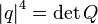 .
.
Комплексными матрицами
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой:
здесь и обозначают комплексно-сопряжённые числа к и .
Такое представление имеет несколько замечательных свойств:
- комплексному числу соответствует диагональная матрица;
- сопряжённому кватерниону соответствует сопряжённая транспонированная матрица:
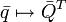 ;
;
- квадрат модуля кватерниона равен определителю соответствующей матрицы:
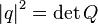 .
.
Связанные объекты и операции
Для кватерниона
кватернион называется скалярной частью а кватернион — векторной частью. Если то кватернион называется чисто скалярным, а при — чисто векторным.
Сопряжение
Для кватерниона сопряжённым называется:
Сопряжённое произведение есть произведение сопряжённых в обратном порядке:
Для кватернионов справедливо равенство
Модуль
Так же, как и для комплексных чисел,
называется модулем . Если то называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль:  .
.
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырёх квадратов вытекает, что иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Обращение умножения (деление)
Кватернион, обратный по умножению к , вычисляется так: .
Алгебраические свойства
Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
- .
Множество кватернионов является примером кольца с делением.
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел. Вообще , , являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел[2].
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение  имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
Кватернионы и повороты пространства
Кватернионы, рассматриваемые как алгебра над , образуют четырёхмерное вещественное векторное пространство. Любой поворот этого пространства относительно может быть записан в виде , где и — пара единичных кватернионов, при этом пара определяется с точностью до знака, то есть один поворот определяют в точности две пары — и . Из этого следует, что группа Ли поворотов есть факторгруппа , где обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно может быть записан в виде , где — некоторый единичный кватернион. Соответственно, , в частности, диффеоморфно .
«Целые» кватернионы
В качестве нормы кватерниона выберем квадрат его модуля:  .
.
Целыми по Гурвицу (также engl) принято называть кватернионы такие, что все — целые и одинаковой чётности.
Целый кватернион называется
- чётным
- нечётным
- простым
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме , нацело (иными словами,  ).
).
Целые единичные кватернионы
Существует 24 целых единичных кватерниона:
- , , , ,
- .
Они образуют группу по умножению и лежат в вершинах правильного четырёхмерного многогранника — кубооктаэдра (не путать с трёхмерным многогранником-кубооктаэдром).
Разложение на простые сомножители
Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема.[3] Для любого фиксированного порядка множителей в разложении нормы кватерниона в произведение простых целых положительных чисел существует разложение кватерниона в произведение простых кватернионов такое, что . Причём данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
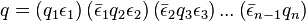 ,
,
где  ,
,  ,
,  , …
, …  — целые единичные кватернионы.
— целые единичные кватернионы.
Например, примитивный кватернион имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
Общее число разложений такого кватерниона равно
Функции кватернионного переменного
Вспомогательные функции
Знак кватерниона вычисляется так:
 .
.
Аргумент кватерниона — это угол поворота четырёхмерного вектора, который отсчитывается от вещественной единицы:
- .
В дальнейшем используется представление заданного кватерниона в виде
Здесь — вещественная часть кватерниона, . При этом , поэтому проходящая через и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид для фиксированного единичного вектора . В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Элементарные функции
Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если для комплексных чисел, то , где кватернион рассматривается в «комплексном» представлении .
- Степень и логарифм
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до .
- Тригонометрические функции
Регулярные функции
Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию как имеющую предел
Оказывается, что все такие функции имеют в некоторой окрестности точки вид
где — постоянные кватернионы. Другой способ основан на использовании операторов
и рассмотрении таких кватернионных функций , для которых[4]
что полностью аналогично использованию операторов и в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов, гармонических функций и рядов Лорана для кватернионных функций[5].
Производная Гато
Производная Гато функции кватернионного переменного определена согласно формуле
Производная Гато является аддитивным отображением приращения аргумента и может быть представлена в виде[6]
Здесь предполагается суммирование по индексу . Число слагаемых зависит от выбора функции . Выражения и называются компонентами производной.
Виды умножений
Умножение Грассмана
Так по-другому называется общепринятое умножение кватернионов ().
Евклидово умножение
Отличается от общепринятого тем, что вместо первого сомножителя берется сопряжённый к нему: . Оно также некоммутативно.
Скалярное произведение
Аналогично одноимённой операции для векторов:
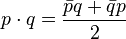 .
.
Эту операцию можно использовать для выделения одного из коэффициентов, например,  .
.
Определение модуля кватерниона можно видоизменить:
- .
Внешнее произведение
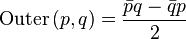 .
.
Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Векторное произведение
Аналогично одноимённой операции для векторов. Результатом является тоже вектор:
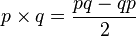 .
.
Из истории
Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам.[8]
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами. Позднее Фробениус строго доказал (1877) теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно.
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[9] Позднее на основе алгебры кватернионов был создан трёхмерный векторный анализ (Гиббс, Хевисайд).
Новые результаты и направления исследований
Кватернионы и метрика Минковского
Как алгебра над , кватернионы образуют вещественное векторное пространство , снабжённое тензором третьего ранга типа (1,2), иногда называемого структурным тензором. Как всякий тензор такого типа, отображает каждую 1-форму на и пару векторов из в вещественное число . Для любой фиксированной 1-формы превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на . Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на . В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы , а соответствующая псевдоевклидова метрика есть метрика Минковского[10]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[11] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[12].
См. также
|
|||||||||||||||||||
| Кватернионы | |||||||||||||||||||
Примечания
- Кватернионы в программировании игр (GameDev.ru)
- ↑ Теорема Фробениуса
- On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, by John H. Conway and Derek A. Smith (англ.). — Review. Архивировано из первоисточника 22 августа 2011. Проверено 7 февраля 2009.
- ↑ R. Fueter Über die analytische Darstellung der regulären Funktionen einer Quaternionenvariablen, — Comment. math. Helv. 8, pp.371—378, 1936.
- ↑ A. Sudbery Quaternionic Analysis, — Department of Mathematics, University of York, 1977.
- ↑ Выражение не является дробью и должно восприниматься как символ оператора. Данное обозначение предложено для того, чтобы сохранить преемственность с классическим анализом.
- ↑ В письме своему сыну Арчибальду от 5 августа 1865 года Гамильтон пишет: «…Но, конечно, надпись уже стёрлась» (Л. С. Полак Вариационные принципы механики, их развитие и применение в физике.— М.: Физматгиз, 1960.— С.103-104)
- ↑ Бурбаки Н.. Архитектура математики. Очерки по истории математики. — М.: Иностранная литература, 1963. — С. 68.
- Отзыв о работах академика П. П. Лазарева.
- ↑ Vladimir Trifonov A Linear Solution of the Four-Dimensionality Problem // Euruphysics Letters, — IOP Publishing, V. 32, № 8 / 12.1995. — С. 621—626 — DOI: 10.1209/0295-5075/32/8/001.
- ↑ Vladimir Trifonov Natural Geometry of Nonzero Quaternions // International Journal of Theoretical Physics, — Springer Netherlands, V. 46, № 2 / 02.2007. — С. 251—257 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).
- ↑ Vladimir Trifonov GR-Friendly Description of Quantum Systems // International Journal of Theoretical Physics, — Springer Netherlands, V. 47, № 2 / 02.2008. — С. 492—510 — ISSN 0020-7748 (Print) ISSN 1572-9575 (Online).
Литература
- И. Л. Кантор, А. С. Солодовников Гиперкомплексные числа. — М.: Наука, 1973. — 144 с.
- Мищенко А., Соловьев Ю. Кватернионы, — Квант, N9, 1983.
- Martin John Baker EuclideanSpace.com — применение кватернионов в 3D графике.
- Кватернионы. Кватеры.
| Числовые системы | |
|---|---|
| Счётные множества |
Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения |
Вещественные () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы |
Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Кватернион.

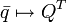 ;
;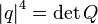 .
.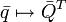 ;
;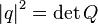 .
.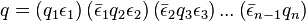 ,
, .
.





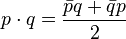 .
.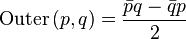 .
.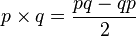 .
.